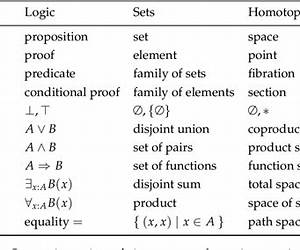
com vs 50 on English Too hard I m dumb English I shouldn t have stayed up reading this but it got exciting Category Theory Set Theory the Integers Reals even Conway s Surreal numbers Cauchy Reals are different to Dedekind Reals unless we want to assume the Law of the Excluded Middle and who wants to do that But Homotopy Type Theory gives us another way to get Real numbers that are fundamentally sound than Cauchy and Dedekind. Introduction to homotopy theory I like a book where the authors assume you re going to read it at least twice you can skip this section on the first reading but it s essential on the second English

Homotopy Type Theory By The Univalent Foundations Program

English

618

ebook

book homotopy type theory ppt

book homotopy type theory pdf free download

book homotopy type theory and practice

book homotopy type theory pdf download

homotopy type theory book

handbook of homotopy theory

from categories to homotopy theory

introduction to homotopy theory

homotopy theories and model categories

homotopy type theory book pdf

homotopy type theory books pdf

homotopy type theory book review

homotopy type theory book pdf download

homotopy type theory books online

introduction to homotopy type theory

Homotopy type theory is a new branch of mathematics that combines aspects of several different fields in a surprising way It is based on a recently discovered connection between homotopy theory and type theory It touches on topics as seemingly distant as the homotopy groups of spheres the algorithms for type checking and the definition of weak groupoids Homotopy type theory offers a new univalent foundation of mathematics in which a central role is played by Voevodsky s univalence axiom and higher inductive types The present book is intended as a first systematic exposition of the basics of univalent foundations and a collection of examples of this new style of reasoning but without requiring the reader to know or learn any formal logic or to use any computer proof assistant We believe that univalent foundations will eventually become a viable alternative to set theory as the implicit foundation for the unformalized mathematics done by most mathematicians Homotopy Type Theory.

[1]

21 on lulu